实验目的

利用决策树预测患者需要佩戴的隐形眼镜类型

这里用了两种方法，方法是用上一节我们自己写的决策树；第二节是调用了sklearn库。

方法1

隐形眼镜数据集是一个公开且著名的数据集，包含患者眼部状况的观察条件以及医生推荐的隐形眼镜类型，数据来源UCI数据库，这里用到的数据集格式如下图：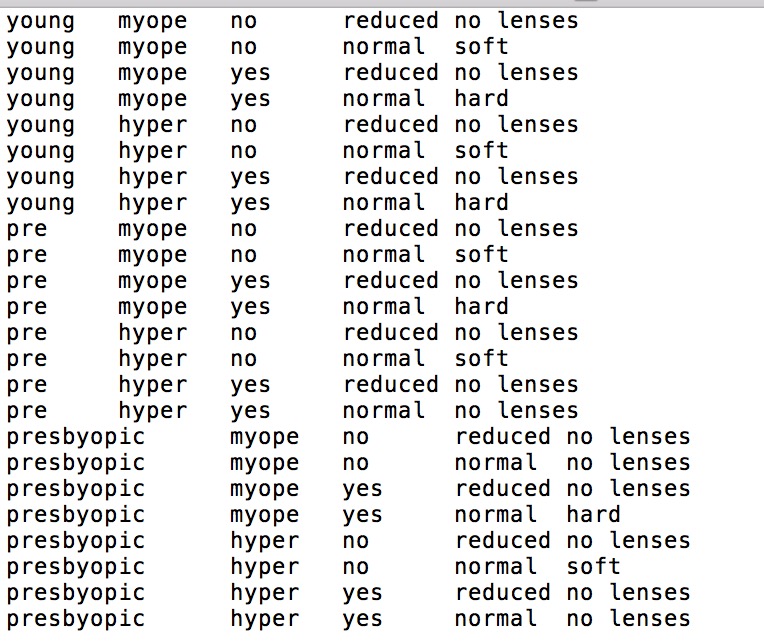

第一列是年龄，第二列是症状，第三列是是否散光，第四列是眼泪数量，第五列是最终的分类标签

数据集的导入

def creatDataSets(filename):
    f = open(filename)
    dataSet = [each.strip().split('\t') for each in f.readlines()]
    labels = ['年龄','症状','是否散光','眼泪','分类标签']
    return dataSet,labels

首先要更新数据集的格式，满足之前手动写的决策树格式

决策树

if __name__ == '__main__':
    filename = 'lenses.txt'
    dataSet,feature = creatDataSets(filename)
    featLabel = []
    myTree = createTree(dataSet,feature,featLabel)
    # 决策树可视化
    #treePlotter.createPlot(myTree)
    # 测试
    testVec = ['normal','yes','hyper','presbyopic','presbyopic','hyper']
    result = classify(myTree,featLabel,testVec)
    print(result)
# ['眼泪', '是否散光', '症状', '年龄', '年龄', '症状']
# no lenses

注意，这里输入测试的数据时，测试数据要与最优特征的顺序一致，也就是代码里的featLabel的格式。
决策树可视化结果如下: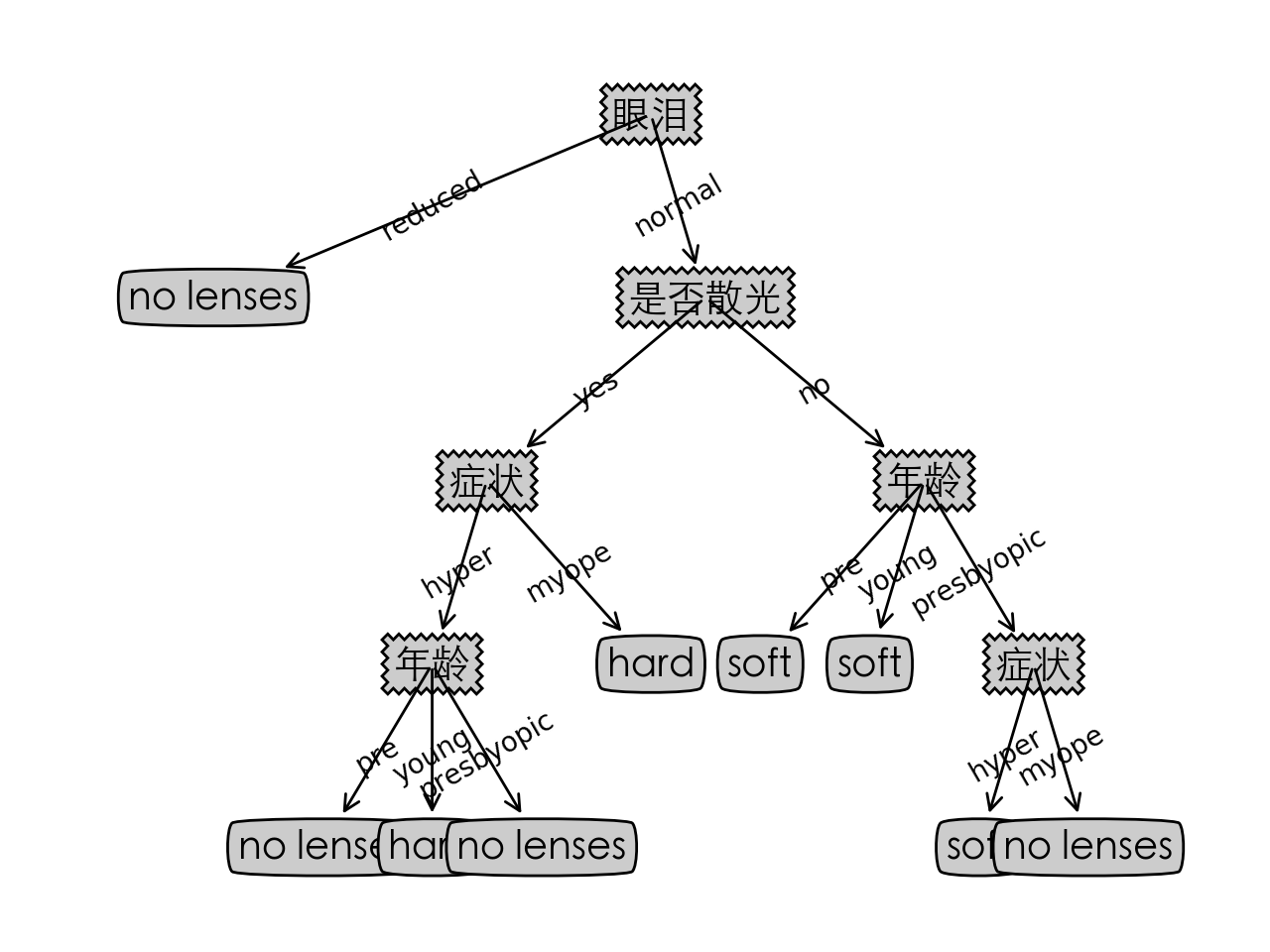

方法2

sklearn.tree提供了决策树的模型，供我们直接调用。

sklearn.tree.DecisionTreeClassifier()函数可以直接构造决策树，一些具体参数解释如下:

criterion:特征选择标准，默认是gini,还可以设置为entropy。gini对应的是CART算法，entropy对应的是ID3算法。
splitter:特征划分点选择标准,默认是best，还可以设置为random。best参数是根据算法选择最佳的切分特征，例如gini、entropy。random随机的在部分划分点中找局部最优的划分点。默认的”best”适合样本量不大的时候，而如果样本数据量非常大，此时决策树构建推荐”random”。
max_features:划分时考虑的最大特征数,默认是None。寻找最佳切分时考虑的最大特征数(n_features为总共的特征数)，有如下6种情况：
1.如果max_features是整型的数，则考虑max_features个特征；
2.如果max_features是浮点型的数，则考虑int(max_features * n_features)个特征；
3.如果max_features设为auto，那么max_features = sqrt(n_features)；
4.如果max_features设为sqrt，那么max_featrues = sqrt(n_features)，跟auto一样；
5.如果max_features设为log2，那么max_features = log2(n_features)；
6.如果max_features设为None，那么max_features = n_features，也就是所有特征都用。
一般来说，如果样本特征数不多，比如小于50，我们用默认的”None”就可以了，如果特征数非常多，我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数，以控制决策树的生成时间。
max_depth:决策树最大深度，默认None。None表示不限制深度，如果特征数过多，建议设置该数值为10-100
max_leaf_nodes：最大叶子节点数，可选参数，默认是None。通过限制最大叶子节点数，可以防止过拟合。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，具体的值可以通过交叉验证得到。
random_state:随机数种子，默认None。
class_weight：类别权重，可选参数，默认是None，也可以字典、字典列表、balanced。指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多，导致训练的决策树过于偏向这些类别。类别的权重可以通过{class_label：weight}这样的格式给出，这里可以自己指定各个样本的权重，或者用balanced，如果使用balanced，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。当然，如果你的样本类别分布没有明显的偏倚，则可以不管这个参数，选择默认的None。

数据处理

读取数据:

1
2
3

import pandas as pd
filename = 'lenses.txt'
data = pd.read_csv(filename,sep='\t',names=['年龄','症状','是否散光','眼泪','分类'])

将数据进行序列化:

from sklearn.preprocessing import LabelEncoder
# 将数据序列化
le = LabelEncoder()  # 创建LabelEncoder()对象，用于序列化
for col in data.columns: # 为每一列序列化
    data[col] = le.fit_transform(data[col])

此时得到的data就是序列化后的。

决策树

dataset = data.iloc[:,0:4].as_matrix() #特征向量                  
label = data.iloc[:,4].as_matrix()  #类别

feature_name = ['年龄','症状','是否散光','眼泪']  # 特征名                 
labelName = ['hard','no lenses','soft'] # 类别名

dtc = DTC(criterion='entropy') # 建立决策树模型                 
dtc.fit(dataset,label)

训练时，DTC(x,y)中x为特征向量，y为分类标签，诸如下列形式：

1 2	X = [[0, 0], [2, 2]] y = [0.5, 2.5]

构建决策树主要就是两步，构建决策树模型以及进行fit训练

可视化

可视化可以用Graphviz来完成。

dot_data = export_graphviz(dtc, out_file=None,                                          
                           feature_names=feature_name,class_names = labelName,          
                           filled=True,rounded=True,                                    
                           special_characters=True                                      
                           )                                                            
graph = pydotplus.graph_from_dot_data(dot_data)                                         
graph.write_pdf('tree.pdf')

得到的结果如下: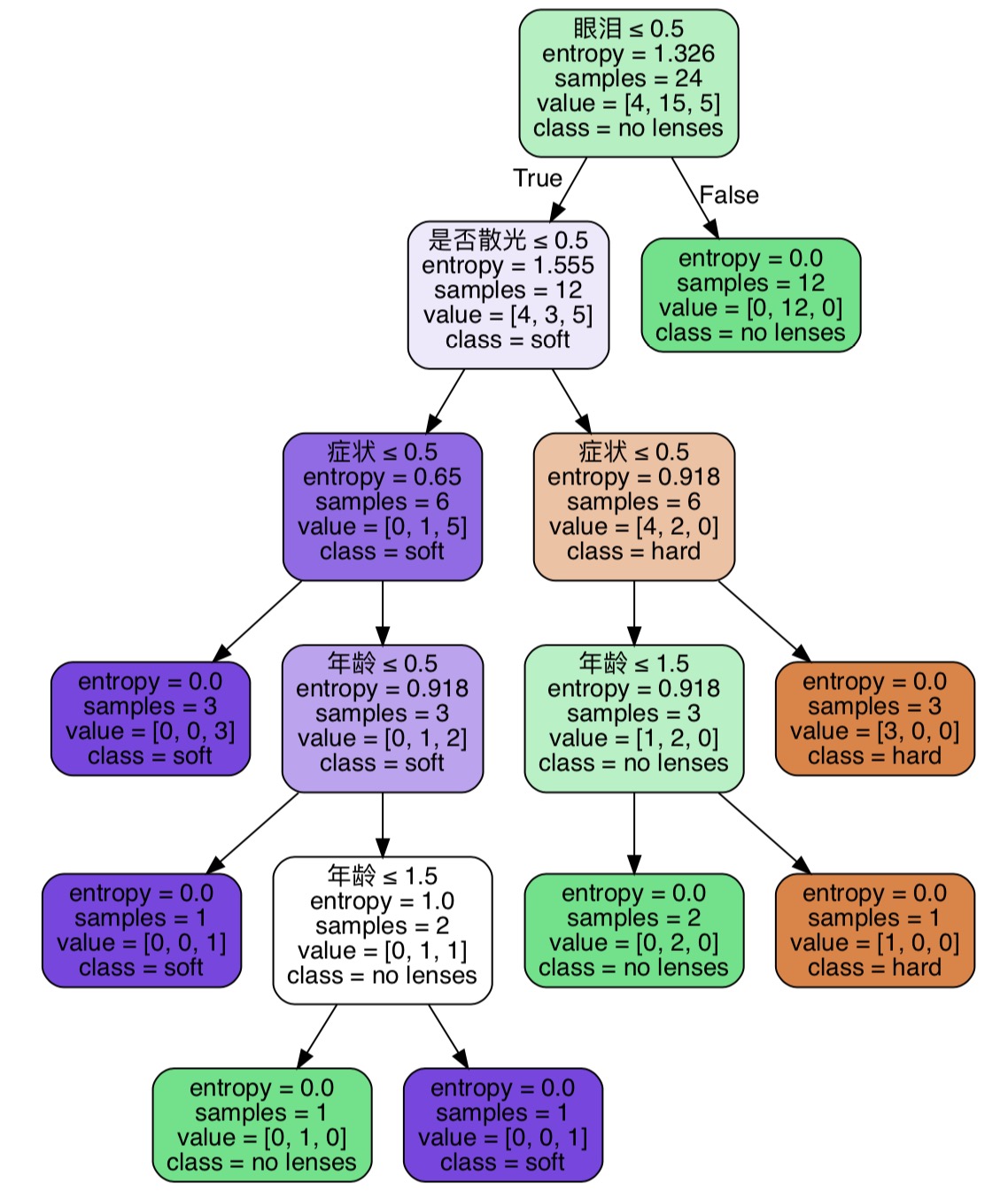

一点说明

关于决策树的实现，可以看这里

利用自己写的决策树完整代码见glasses.py
调用sklearn的完整代码见glasses_sklearn.py