决策树在分类、预测、规则提取等领域有着广泛作用,对于非线性关系的变量筛选方面有着重要作用。下面就简单的介绍一下决策树有关的几种算法及其应用。
决策树
树状结构,叶子节点代表一个分类,非叶节点代表某个属性的划分,根据样本在该属性上的不同取值将其划分为若干子集。
对于分类问题,从已知类标的训练样本中学习并构造决策树是一个自上而下的过程。从根节点开始,对样本的某一特征进行测试,根据测试结果将样本分配到子结点,此时每个子结点对应着该特征的一个取值,如此递归进行,直到到达叶子结点,将样本分到各个叶子结点的分类中。
下面这张取自大水牛博客的图大概能看出决策树的构建方式了(自上而下、递归、分而治之)。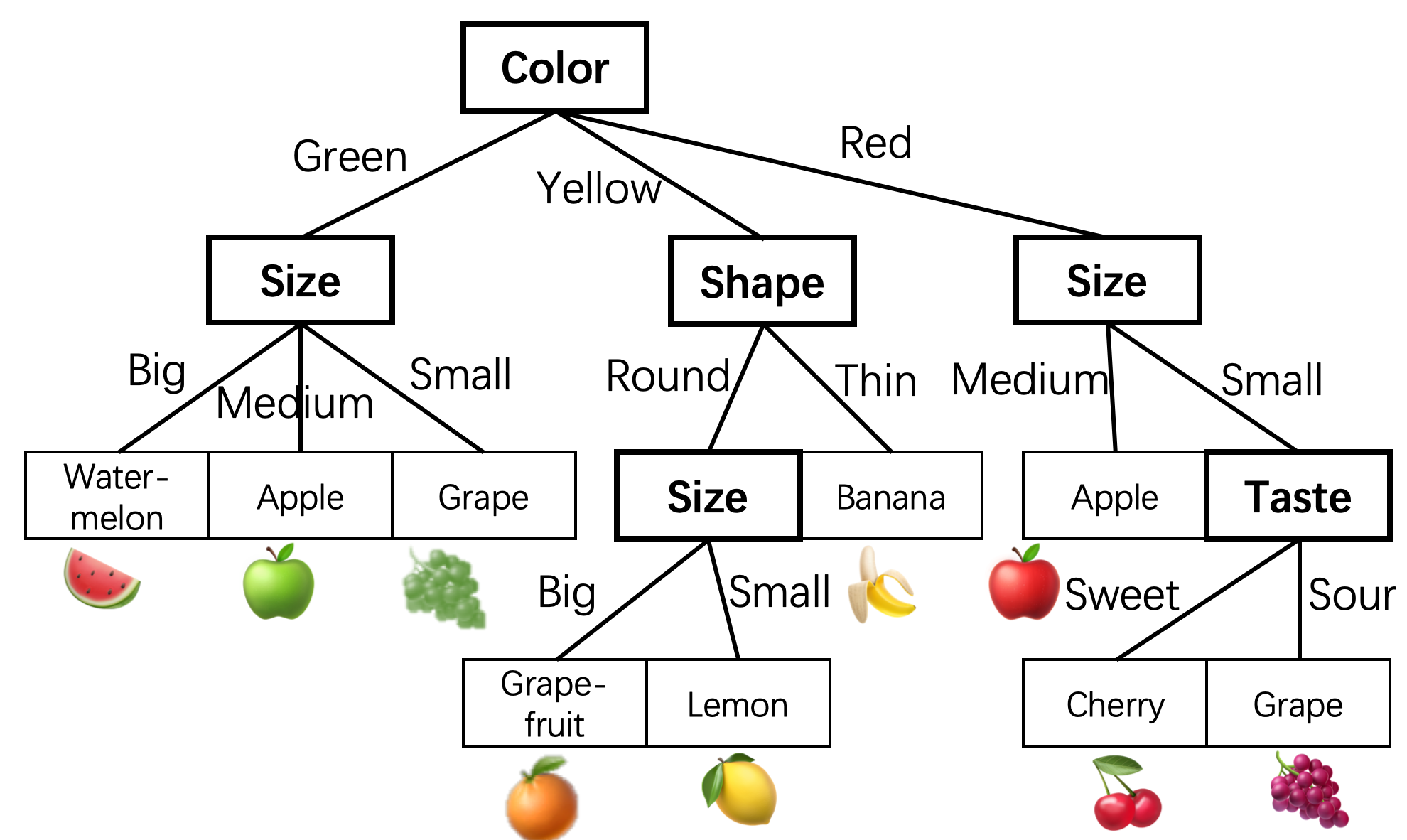
决策树的思想,实际上就是寻找最纯净的划分方法,通俗的说就是把目标分类分的足够开。这个纯度,可以看作是特征选择准则,比如信息增益、信息增益率、基尼系数。使用某特征对子集进行划分后,各个子集的纯度要比划分之前的纯度高(不确定性要比划分前低)
tip:划分后的纯度为各个子集的纯度加权和(子集占比*子集的经验熵)
特征选择准则。
熵:度量随机变量的不确定性
熵可以表示样本集合的不确定性,熵越大,表示样本的不确定性越大。
假设随机变量为X,可能取值为$x_1,x_2,…,x_n$,对于每一个可能的取值$x_i$,其概率为$P(X=x_i)=p_i,(i=1,2,…,n)$,那么我们定义随机变量X的熵为:
经验熵:熵中的概率由数据估计(特别是最大似然估计)得到时,所对应的熵称为经验熵
条件熵:条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性,随机变量X给定的条件下随机变量Y的条件熵(conditional entropy) H(Y|X),定义X给定条件下Y的条件概率分布的熵对X的数学期望:
信息增益
定义:以某种特征划分数据集前后的熵的差值
决策树会把每个特征都尝试一遍,选取一个信息增益最大的特征作为子结点的属性。
简单解释一下,对于待划分的数据集,其熵是一定的,根据某个特征划分后得到的子集,如果熵越小,说明不确定性越小,也就是纯度越高,我们就是希望划分后的子集的纯度越高越好,因为这样对于我们构建决策树可以更快的到达纯度更高的集合,所以要选择前后熵值相差大的特征(即信息增益大)作为划分点,这一思想与梯度下降寻找函数值减小最快的思想类似。
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即:
总之记住一点,如果以信息增益作为特征划分准则,总是选择信息增益大的特征来划分当前数据集。
不过,缺点就是对于取值较多的特征来说,因为该特征的取值很多,所以利用此特征划分更容易得到纯度更高的子集,信息增益比较偏向取值较多的特征。改进就是下面要说的信息增益率了。
信息增益率
其中的$H_A(D)$,对于样本集合D,将当前特征A作为随机变量(取值是特征A的各个特征值),求得的经验熵。
基尼系数
也称基尼不纯度,表示在样本集合中一个随机选中的样本被分错的概率
gini系数越小,代表样本被分错的概率越小,也就是说集合的纯度越高。
代码实现
下面例子参考呆呆的猫。
下表是一个关于银行是否放贷的数据,我们自己编写code来简单的实现一下上述特征选择准则,以便加深理解。
| 年龄 | 有无工作 | 有无房子 | 信贷情况 | 是否给贷款 |
|---|---|---|---|---|
| 青年 | 无 | 无 | 一般 | 否 |
| 青年 | 无 | 无 | 好 | 否 |
| 青年 | 有 | 无 | 好 | 是 |
| 青年 | 有 | 有 | 一般 | 是 |
| 青年 | 无 | 无 | 一般 | 否 |
| 中年 | 无 | 无 | 一般 | 否 |
| 中年 | 无 | 无 | 好 | 否 |
| 中年 | 有 | 有 | 好 | 是 |
| 中年 | 无 | 有 | 非常好 | 是 |
| 中年 | 无 | 有 | 非常好 | 是 |
| 老年 | 无 | 有 | 非常好 | 是 |
| 老年 | 无 | 有 | 好 | 是 |
| 老年 | 有 | 无 | 好 | 是 |
| 老年 | 有 | 无 | 非常好 | 是 |
| 老年 | 无 | 无 | 一般 | 否 |
1 | from math import log |
常用的决策树算法有ID3、CATR()、C4.5,它们分别以上述特征选择准则来构造决策树对目标进行分类,其中ID3算法是最经典的决策树算法。下面依次进行介绍。
ID3
核心:在决策树的各级节点上,使用信息增益方法作为属性的选择标准。
只能处理离散的描述属性。
算法简介
采用信息增益来度量不确定性,信息增益越大,不确定性越小;反之亦然。所以,ID3在每个非叶结点选择信息增益最大的属性作为测试属性。
具体流程
step1:对当前样本集合,计算所有属性的信息增益;
step2:选择信息增益最大的属性作为测试属性,把测试属性取值相同的样本划分为同一个样本子集;
step3:若样本子集的类别属性只含有单个属性,那么该分支为叶子节点;如果不是,递归调用该流程。
实例:分析天气、是否周末、是否促销对餐饮销量的影响
对于天气属性,’多云‘、’多云转晴‘、’晴‘这些属性值相近,均是适合外出的天气,不会对销量有太大的影响,天气属性值设为好;对于下雨等不适合外出的天气设定为坏。
对于是否周末属性,周末设定为是,周内则设定为否。
对于是否有促销活动属性,同周末。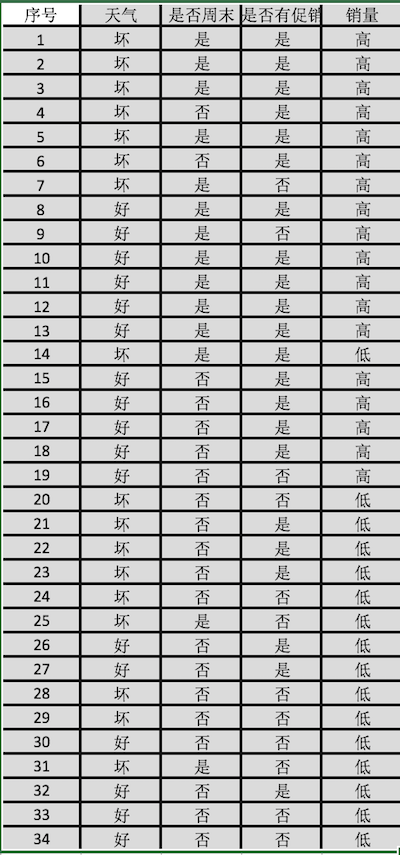
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27#-*- coding: utf-8 -*-
import pandas as pd
data_path = '/Users/apple/Desktop/python_study/图书配套数据、代码/chapter5/demo/data/sales_data.xls'
data = pd.read_excel(data_path,index_col='序号')
#将属性值转换为数据
#1表示好,0表示坏
#1表示是,0表示否
#1表示高,0表示低
data[data=='好'] = 1
data[data=='是'] = 1
data[data=='高'] = 1
data[data!=1] = 0
x = data.iloc[:,:3].as_matrix().astype(int) #样本
y = data.iloc[:,3:].as_matrix().astype(int) #类别
from sklearn.tree import DecisionTreeClassifier as DTC
dtc = DTC(criterion='entropy') #建立决策树模型,基于信息熵 默认是gini
dtc.fit(x,y) #训练模型
#生成决策树 可视化
from sklearn.tree import export_graphviz
import pydotplus
dot_data = export_graphviz(dtc, out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("tree.pdf")
所画出的决策树如下图所示【未修改特征名,可以自行修改dot_data,再生成决策树的pdf】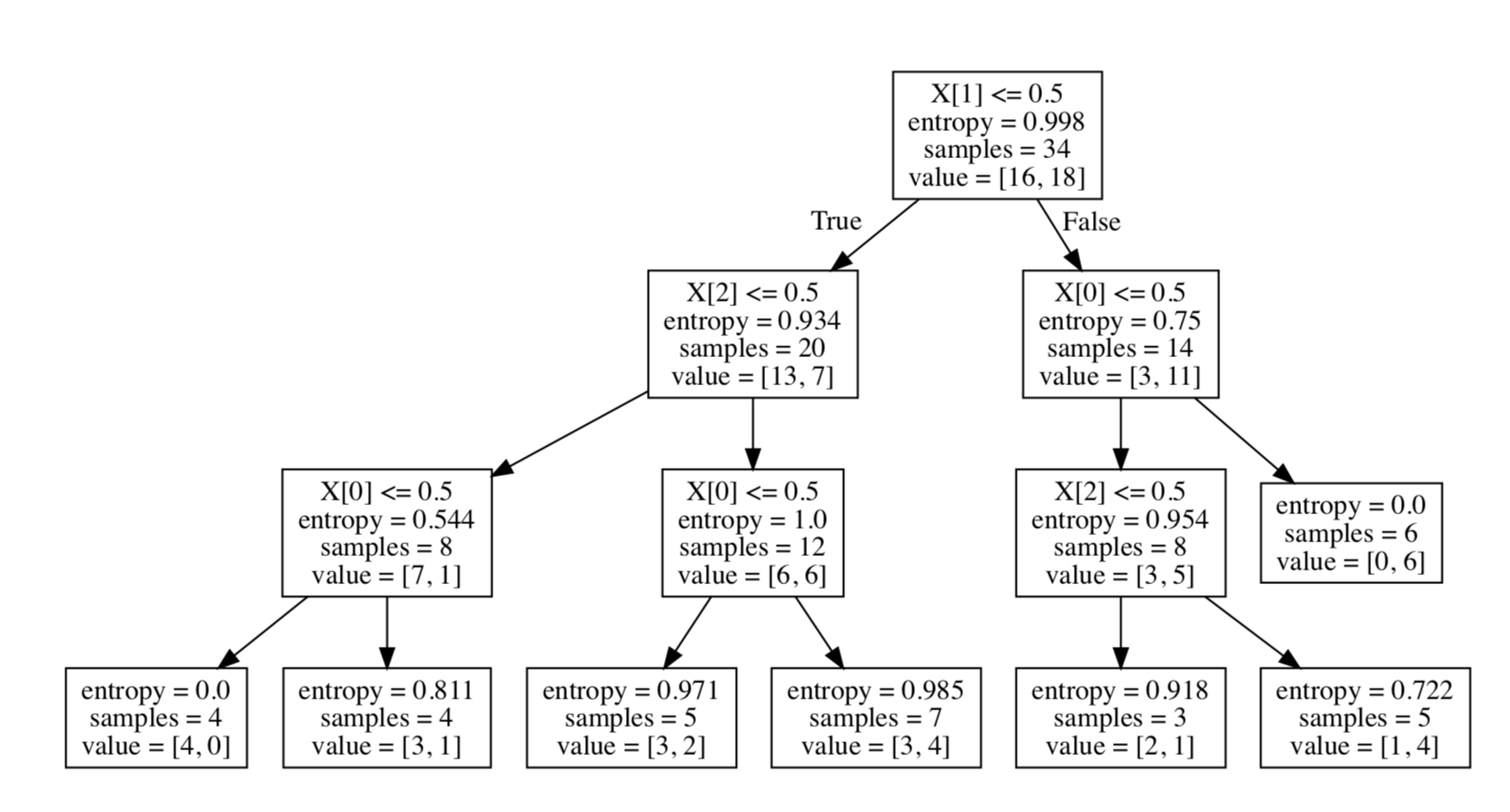
CART
是一种非参数分类和回归方法,通过构建树、修建树、评估树来构建一个二叉树。
如果终结点是连续变量,则为回归树;如果是分类变量,则为分类树。
值得注意的是,由于CART是二叉树,所以根据某特征划定的样本集合只有两个集合:等于给定的特征值、不等于的给定的特征值
对于一个具有多个取值(超过2个)的特征,需要计算以每一个取值作为划分点,对样本D划分之后子集的纯度$Gini(D,A_i)$,(其中$A_i$表示特征A的可能取值),然后选择Gini系数最小的特征作为划分点。
C4.5
使用信息增益率来选择节点属性。
是ID3的一种改进,既能处理离散属性又能处理连续属性。
C4.5 处理连续特征是先将特征取值排序,以连续两个值中间值作为划分标准。尝试每一种划分,并计算修正后的信息增益,选择信息增益最大的分裂点作为该属性的分裂点。